Exporting A Render With Transparency In A Way That Supports Blending
Recently I ran into an interesting issue at work which led to a pretty neat solution. The renderer I was working with is capable of exporting the contents of the viewport to an image by rendering them to a buffer and saving the resulting color and alpha to disk. There is an issue with this approach though: if both the background and some of the rendered meshes are transparent, the resulting image will not look correct when blended afterwards. Is there a way to save an image that will still support blending? Lets find out.
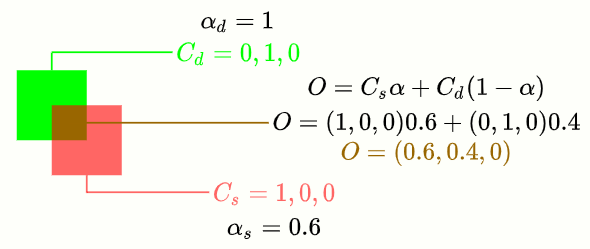
Alpha blending
To understand this behavior I decided to look at how the colors were produced both for the renderer and for the exported image. First lets remind ourselves how alpha blending works. If we want to blend a transparent color (called the source color) with a background color (called the destination), we first define an \(\alpha\) parameter that determines how transparent the source is (\(\alpha = 0\) is fully transparent, \(\alpha = 1\) is fully opaque). Then we use the so called over operator to compute the final color (basically a linear interpolation):
\[O = \alpha C_s + (1 - \alpha) C_d\]Computing the color of the blended image
With this in mind, lets see how the color of the (incorrectly) blended image is computed. Say our renderer exported an image with color \(C_i\) and alpha \(\alpha_i\), if we blend the image with a background layer of color \(B_i\) the result is
\[O_i = \alpha_i C_i + (1 - \alpha_i) B_i\]
Since \(C_i\) is the final color of the rendered image, this equation will produce a clearly different result unless we force \(\alpha_i = 1\), which would make the image opaque and therefore not able to be blended.
Computing the color of the rendered scene
Lets take note of this result and see how our renderer arrives at the color \(C_i\). Typically in a scene with overlapping objects with different levels of transparency, objects are rendered back to front and blended with the over operator. So if we have a background of color \(B_r\) and we render the first transparent object (\(C_0\), \(\alpha_0\)) over it, the resulting color will be
\[O_0 = \alpha_0 C_0 + (1 - \alpha_0) B_r\]This result is then placed in the backbuffer. Rendering a second object (\(C_1\), \(\alpha_1\)) will result in it being blended with the previous result
\[O_1 = \alpha_1 C_1 + (1- \alpha_1) \cancelto{\alpha_0 C_0 + (1 - \alpha_0) B_r}{O_0}\] \[O_1 = [\alpha_1 C_1 + (1- \alpha_1) (\alpha_0 C_0)] + [(1- \alpha_1) (1 - \alpha_0)] B_r\] \[O_1 = X_1 + K_1 B_r\]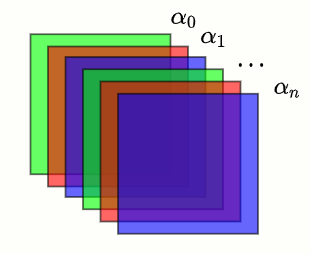
If we repeat this \(n\) times we’ll get
\[O_n = X_n + K_n B_r\]where \(X_n\) is a constant term and
\[K_n = (1 - \alpha_n) (1 - \alpha_{n-1}) ... (1 - \alpha_0)\]The final rendered color is then \(O_r = O_n\) which gets saved as \(C_i\).
Fixing the issue
What we want to achieve is for the color of the blended image equal to be equal to the final rendered color for any background \(B\). So we have to find a different \(C_i\) and \(a_i\) such that for any background color \(B_n = B_r = B\) we’ll have \(O_i = O_r\). Substituting for the equations above we get
\[a_i C_i + (1 - \alpha_i) B = X_n + K_n B\]which we can solve for \(C_i\)
\[C_i = \frac{X_n}{\alpha_i} + \frac{B}{\alpha_i} (K_n + \alpha_i - 1)\]Since we can’t solve the equation with two unknowns (\(C_i\) and \(\alpha_i\)), we set \(\alpha_i\) in a way that simplifies the equation
\[K_n + \alpha_i - 1 = 0\] \[\alpha_i = 1 - K_n\]making
\[C_i = \frac{X_n}{\alpha_i}\]
And that’s it. Instead of writing the color of our rendered buffer directly to disk, we compute \(K_n\) and modify the color \(C_i\) and alpha \(\alpha_i\) before writing to an image. Now, you might recall that \(K_n\) involves the product of a bunch of different alpha values. We could figure out all the alphas involved and carry out the multiplications, or we could use a little trick. If we first render the scene with \(B = 0\), we get
\[O_{B0} = X_n + K_n \cancelto{0}{B}\] \[O_{B0} = X_n\]If we then render again with \(B = 1\), we get
\[O_{B1} = X_n + K_n \cancelto{1}{B}\] \[O_{B1} = X_n + K_n\]meaning we can get the value of \(K_n\) by subtracting these two colors
\[K_n = O_{B1} - O_{B0}\]And now we’re done. Rendering the scene twice might be expensive in some cases, but it simplifies things so much that I still chose to go with this solution.
Step-by-step solution
To summarize, in order to save an image of a render with transparency in a way that it can still be blended afterwards we do the following:
- Render the scene with a white background to buffer 1
- Render the scene with a black background to buffer 2
- For each pixel, get the value of \(K_n\) by subtracting the color in buffer 1 from the color in buffer 2
- For each pixel, calculate a new alpha \(\alpha_i\) using the formula \(\alpha_i = 1 - K_n\)
- For each pixel of buffer 2 with color \(C = X_n\), calculate a new color \(C_i\) using the formula \(C_i = \frac{C}{\alpha_i}\)
- Save \(C_i\) and \(\alpha_i\) to disk